Nonadiabatic Dynamics
Nonadiabatic dynamics are necessary when the Born-Oppenheimer approximation is not valid. In order to describe these dynamics, we are developing new methods including nonadiabatic version of ring-polymer molecular dynamics and an instanton extension of Marcus theory which applies to anharmonic quantum systems. The method can also be applied to compute vibronic spectra.
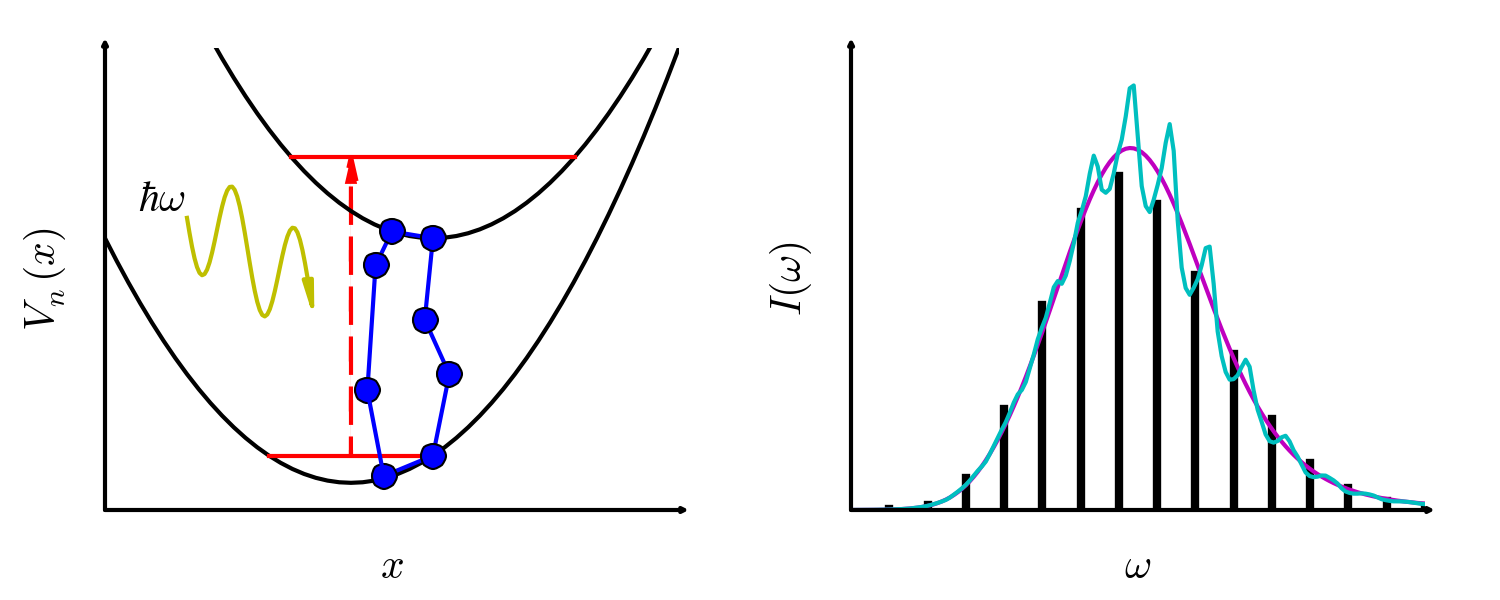
The mapping approach
One crucial challenge in simulating nonadiabatic dynamics revolves around treating both the continuous nuclear phase space as well as the discrete space of electronic states. The mapping approach allows these two to be combined in a single, extended phase space, which is easier to sample and explore with classical trajectories. As a result, semiclassical methods employing the mapping approach can be applied to large, condensed phase systems, inaccessible to wavefunction based quantum dynamics methods.
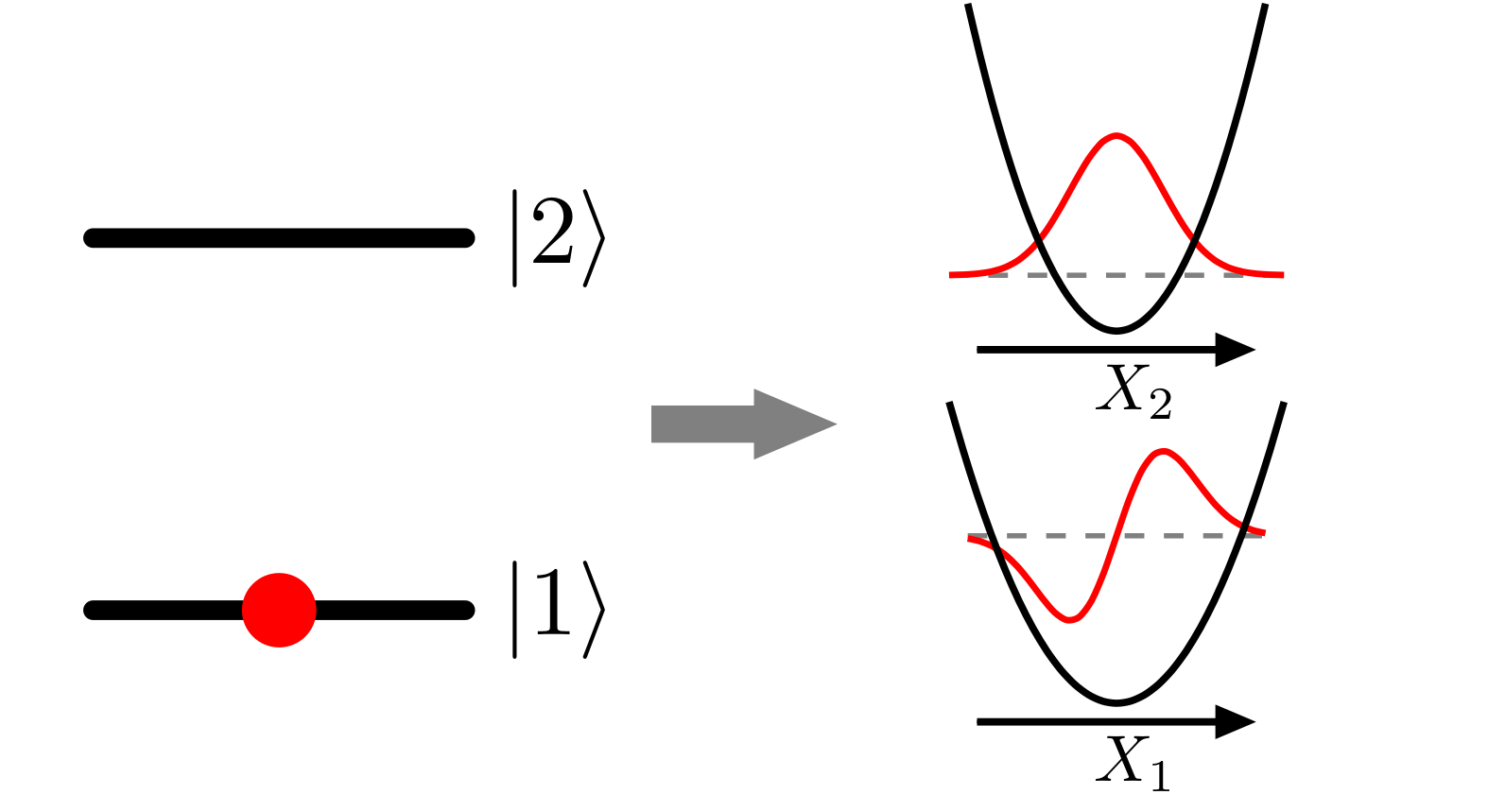
Fixing semiclassical dynamics methods
Traditional semiclassical dynamics methods rely on a definition of the electronic population operator which has a non-zero trace. In addition to resulting in a certain extent of ambiguity with respect to what the value of the trace should be, this introduces a significant error in the long time limit.
We have derived an alternative definition of the electronic population operator, by splitting it into two parts. One is simply the identity, the other other has a trace of zero. Using the knowledge of how the identity operator behaves in quantum mechanics, we can simply set it to 1 in classical mechanics.
This approach not only eliminates the ambiguity with respect to the trace of the population operator, but also avoids the error associated with the semiclassical approximation for the identity, as we use an exact value instead.
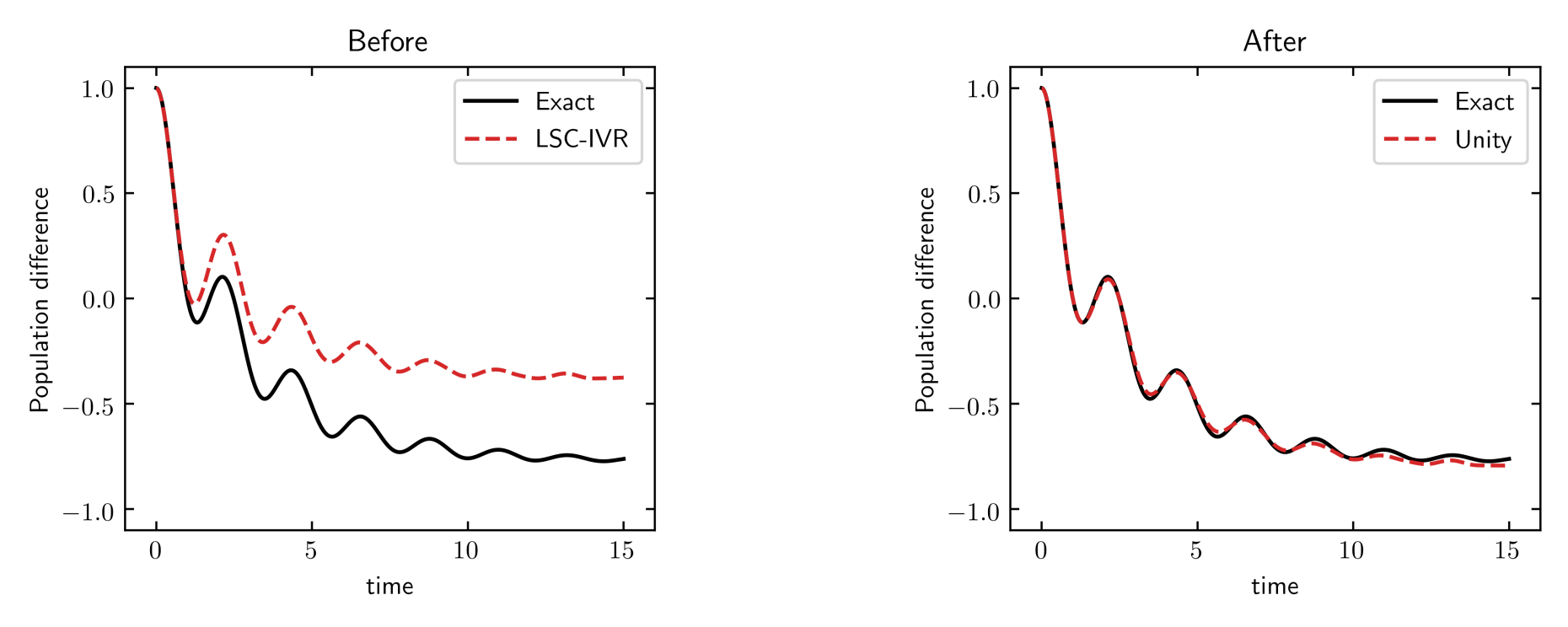
Standard semiclassical methods fail to capture nonadiabatic dynamics in the long time limit. Using our unity definition of the identity drastically improves results. The result of applying our unity approach to the population dynamics of asymmetric spin-boson systems is considerable. Traditional semiclassical approaches such as LSC-IVR yield highly incorrect results in the long time limit. Our simple modification fixes this problem, yielding results in close to quantitative agreement with exact quantum benchmarks. Importantly, our approach can be applied to any Hermitian operator and is trivially generalised to any number of electronic states.