New paper shows how to describe quantum entanglement with classical trajectories

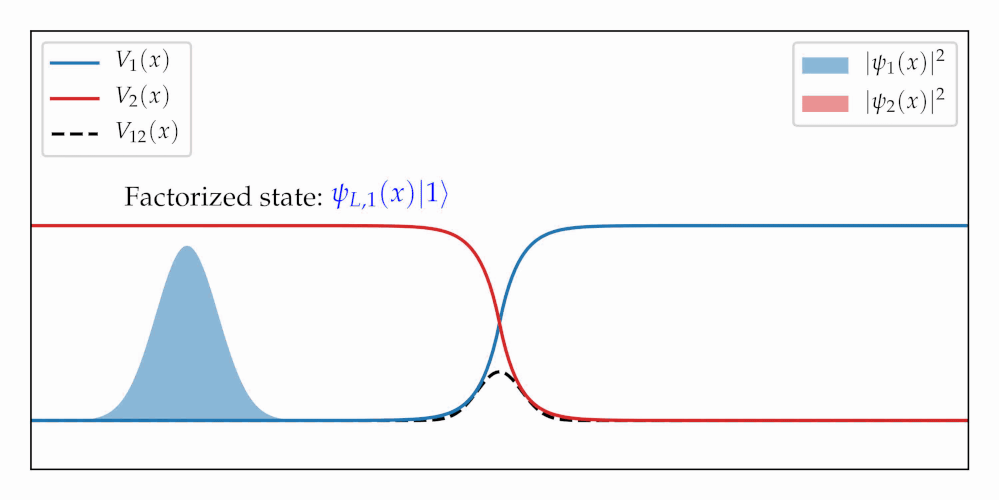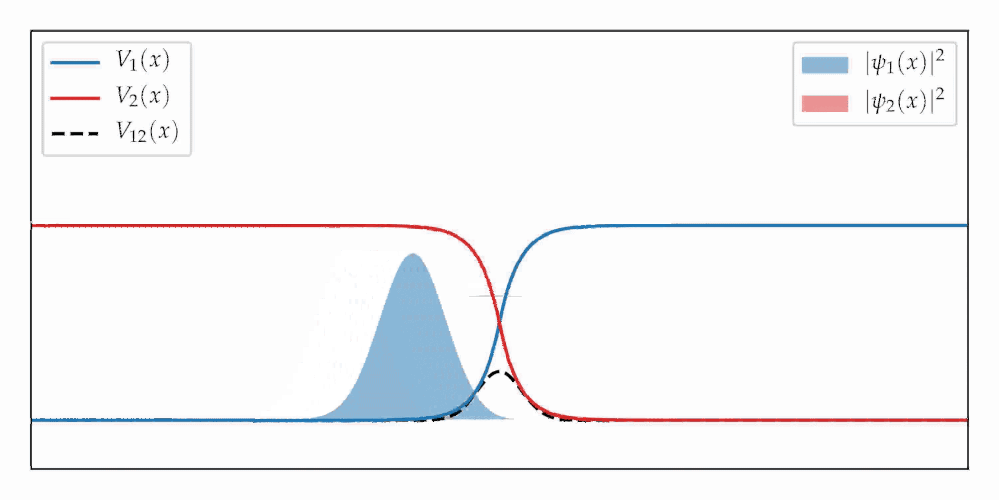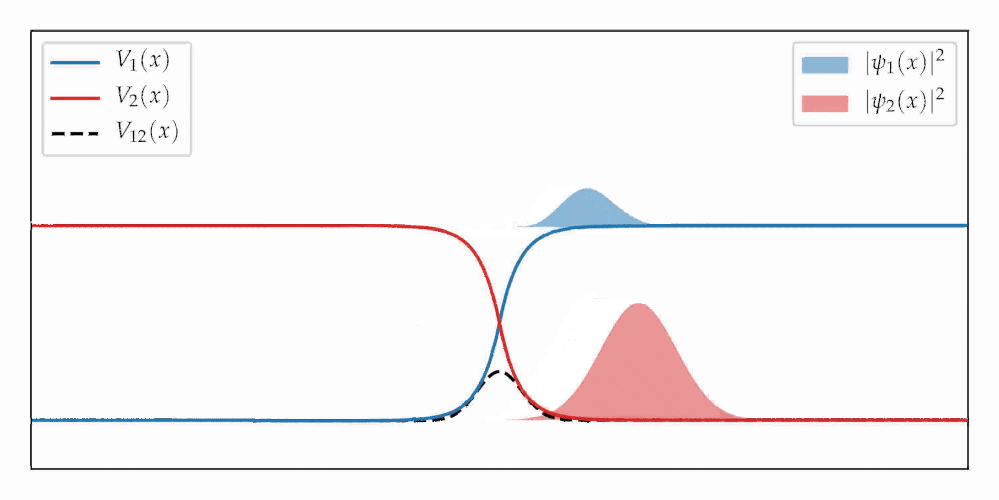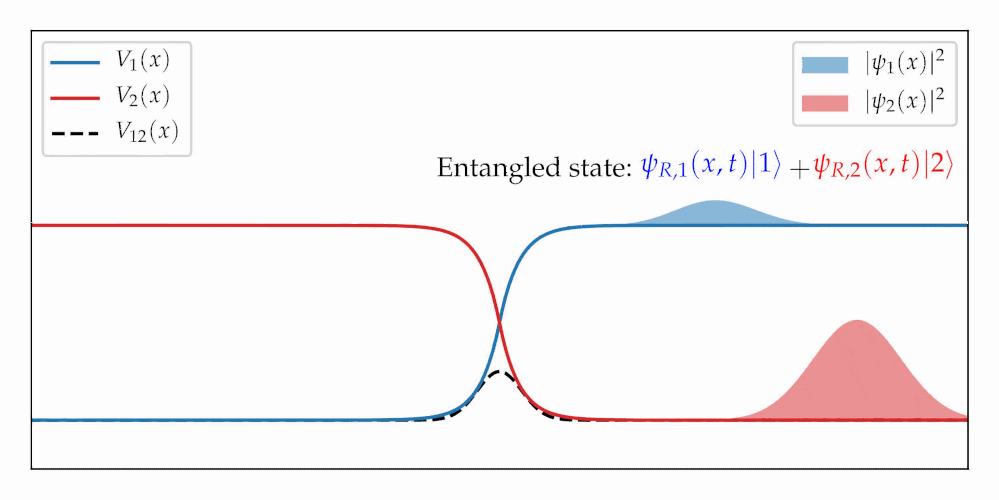
When a wavepacket passes through a region with coupled potential energy surfaces, it splits into a fast and a slow-moving part (see first figure). The splitting is an example of entanglement creation between nuclear and electronic degrees of freedom, and entanglement is a quantum-mechanical concept. Does this mean that one cannot simulate this process classically?

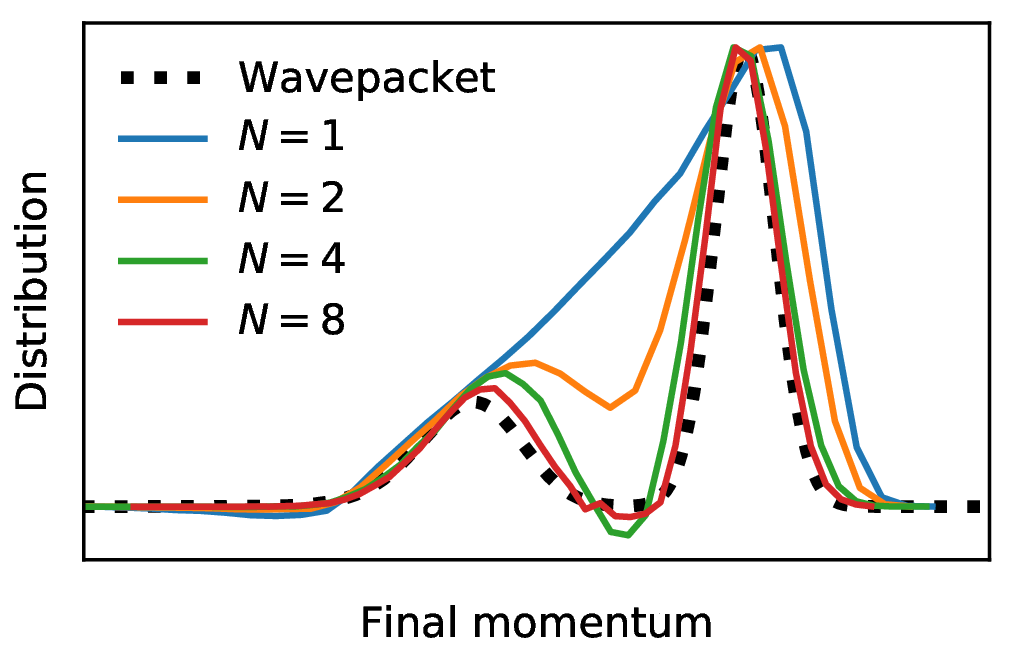
If by “classical” we mean that the simulation consists of Hamiltonian trajectories that are uncoupled, deterministic, and phaseless, then this was until recently believed to be impossible. In a new paper, we have however demonstrated that if the trajectories are weighted by a certain function called the “universal function”, then they can recover the correct entangled state despite evolving independently of each other. The universal function describes the statistics of N spins that represent the two-level system and increasing N leads to wavepacket splitting (see second figure), with a low computational effort. Further exciting examples and details of the method are found just a click away: